Research

During graduate school at Indiana University, I studied triply periodic minimal surfaces with my advisor, Matthias Weber. My dissertation was centered on finding deformations of these surfaces. In particular, I proved that two minimal surfaces (the gyroid and the lidinoid) admit deformations. In the meantime, check out the Indiana University Virtual Minimal Surface Museum for tons of great pictures. (Click on "Archive".)

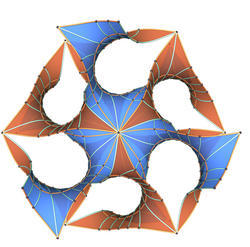
The gyroid is a triply periodic minimal surface that contains no straight lines or planar symmetry curvers. It was discovered by Alan Schoen in 1970 and was proven embedded by Grosse-Brauckman and Wohlgemuth (1995). The lack of symmmetries make the gyroid hard to visualize -- I think that the best way to understand it is to look at a rotatable 3-D model (or maybe to have a sculpture in your office). The gyroid has a host of physical applications, among them understanding ketchup, materials science, and modeling the microstructures of cells.

Papers / Publications

(with A. Neath, J. Cavanaugh) Model evaluation, discrepancy function estimation, and social choice theory. to appear in Computational Statistics.
(with K. Lawson, J. Parish, C. Traub) Coloring graphs to classify simply closed geodesics on polyhedra. Int. J. Pure Appl. Math. 89 (2013), no. 2, 123-129
(with M. Feldman and M. Quivey) Intel Math Connections: A Three-Year Study of the Impact of a Math-Based Program on Elementary Teachers 2013 ASQ Advancing the STEM Agenda Conference Proceedings.
A real-life data project for an interdisciplinary math and politics course PRIMUS: Problems, Resources, and Issues in Mathematics Undergraduate Studies (2012), 23:1, 13-24
(expository article) Meet the Gyroid. Published online by Plus Magazine, an expository mathematics magazine for students.
A note on some upper bounds for permanents of (0,1)-matrices. J. Interdiscip. Math. 12 (2009) no. 1, 123-128.
Deformations of the gyroid and Lidinoid minimal surfaces. Pacific J. Math. 235 (2008), no. 1, 137--171.
New Families of Embedded Triply Periodic Minimal Surfaces of Genus 3 in Euclidean Space. Ph.D. thesis. August 4, 2006.

Computer imaging

Images of Casey Douglas' doubly periodic, Genus 1 sheared Scherk surfaces (Mathematica file, 6 stills, and 600x600 mp4 movie showing the deformation)

Master's theses

Shuai Hao ``An introduction to discrete minimal surfaces via the Enneper surface.'' July 2013.
Paul Heidbrink ``A two parameter family of embedded triply periodic minimal surfaces.'' August 2011.
Darren Garbuz ``Isoperimetric properties of some genus three triply periodic minimal surfaces embedded in Euclidean space.'' May 2010.

Talks

Slides from an invited talk to the St. Mary's College of Maryland MRS (mathematical research seminar) (March 2010 (50 mb file)
Slides from an invited talk to the St. Mary's College of Maryland math club (March 2010) (50 mb file)
Slides from Mathfest 2009 in Portland, OR (August 2009)
Slides from the AMS Central Section Meeting in Bloomington, IN (April 2008)
Slides from the AMS/MAA Joint Meetings in San Diego (January 2008)
Slides from the Illinois State Mathematics Association of America (ISMAA) 2007 meeting (March 30, 2007)
Slides from the AMS/MAA Joint Meetings in New Orleans (January 2007)
Slides from the job-talk I gave at Southern Illinois University Edwardsville (March 7, 2006)
Slides from a rather low-key talk I gave at the very hospitable Lenoir-Rhyne College (Februrary 9, 2006)
Slides from the Eastern Illinois University Colloquium (January 20, 2006)

download

Relevant Minimal Surfaces Links

POV Ray is a very nice raytracer program that can be used to create wonderful pictures. We use Mathematica to export a mesh: see my advisor's Mathematica package.
A number of examples and images of triply periodic minimal surfaces made with Brakke's Surface Evolver.
The Virtual Museum of Minimal Surfaces
Some other mathematicians whose work involves minimal surfaces include: Matthias Weber, Mike Wolf, Martin Traizet, and the Granada group.