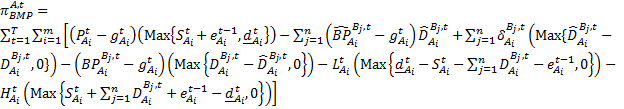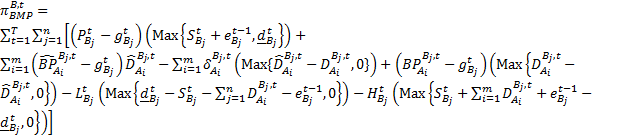A Best
Matching Protocol for Collaborative Energy Distribution Networks
Ehsan Jahanpour
and Hoo Sang Ko
Industrial and Manufacturing Engineering,
Southern Illinois University Edwardsville
In
a sustainable wind energy distribution network, energy price is another parameter that influences the
providers¡¯ and communities¡¯ collaboration in the network in addition to generation and
distribution constraints. General frameworks have been developed to model the
electricity price in an energy market [1-3]. For example, Botterud et al. [3] proposed a model for optimal trading
of wind power in the market based on one-day-ahead forecasts and real-time demands. The Best
Matching Protocol (BMP) intends to define the most efficient
bidding price and matches the best energy providers in order to maximize the
long-term profit of the energy providers (both roles A and B) in the network.
Suppose that a demand set 
to be received by community 
, where 
is the demand that has been assigned to
deliver to the community from provider 
on one day ahead of day 
. Other notations used in the model
include:
expected demand from community on day
electricity price sold to community by its corresponding provider on day
electricity generation cost of provider on day
electricity amount supplied by provider on day
excessive electricity of provider on day
electricity price bid offered from provider 
to provider one day ahead of day
damage cost for not being able to fulfill shared capacity
paid by provider on day
real-rime electricity supplied by provider to provider on day
real-time electricity price from provider to provider on day
penalty cost for the lost demand paid by provider day
holding cost of the excessive electricity stored by provider
day
Based on the shared
information between providers and their expected profit, BMP will match the
shared demand with the shared capacity so that the demand can be fulfilled and
also the provider¡¯s profit can be maximized. In other words, BMP will
function such that the profit of role A and role B providers, shown in Equations (1) and (2), can be maximized. The provider roles are dynamic so a provider could be of
role A on a day and of role B on another day.
|
|
(1) |
|
|
(2) |
The BMP will match the best pair (a Î A, b Î B) by solving
the optimization problem to deal with the overall waste in the network of wind
farms. This BMP must work in conjunction with the Demand and Capacity Sharing
Protocol (DCSP) [4] for collaboration in the distribution network.
[1]
A. Botterud, Z. Zhou, J. Wang, R. J. Bessa, H. Keko, J.
Sumaili, and V. Miranda, "Wind power trading
under uncertainty in LMP markets,"
IEEE Transactions on Power Systems, vol. 27, no. 2, pp.
894-903, 2012.
[2]
E. Litvinov, "Design and operation of the locational
marginal prices-based electricity markets," Generation, Transmission
& Distribution, vol.
4, no. 2, pp. 315-323, 2010.
[3]
J. C. Smith, S. Beuning, H. Durrwachter,
and E. Ela, "Impact of variable renewable energy on US electricity
markets," in Proc. of IEEE Power and
Energy Society General Meeting, Minneapolis, MN, 2010.
[4]
Yoon, S.W. and Nof, S.Y. (2010). Demand and capacity sharing
decisions and protocols in a collaborative network of enterprises. Decision
Support Systems, 49(4), 442-450.