DIJKSTRA'S ALGORITHM
void dijkstra(graph g, tree& t, node root)
vertex v, w
edge e
heap h
t.edges := empty
t.nodes := {root}
h.makeheap(g.incident(root)) // can use repeated inserts
do (e := h.deletemin()) 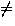 empty
empty 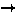 t.edges := t.edges
t.edges := t.edges 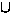 {e}
v := e.new_node
t.nodes := t.nodes
{e}
v := e.new_node
t.nodes := t.nodes 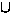 {v}
for w
{v}
for w 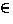 g.adj(v)
g.adj(v) 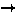 if w
if w  t.nodes and w
t.nodes and w  h
h 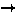 e.old_node := v
e.new_node := w
e.dist := t.dist(v)+ g.cost(v, w)
h.insert(e)
| w
e.old_node := v
e.new_node := w
e.dist := t.dist(v)+ g.cost(v, w)
h.insert(e)
| w 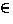 h and g.cost(v,w) + t.dist(v) < h.dist(w)
h and g.cost(v,w) + t.dist(v) < h.dist(w) 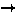 h.changekey(w, (t.dist(v)+g.cost(v,w)), v)
fi
rof
od
end dijkstra
h.changekey(w, (t.dist(v)+g.cost(v,w)), v)
fi
rof
od
end dijkstra
Bernard Waxman
11/11/1997
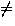 empty
empty 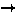 t.edges := t.edges
t.edges := t.edges 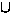 {e}
v := e.new_node
t.nodes := t.nodes
{e}
v := e.new_node
t.nodes := t.nodes 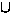 {v}
for w
{v}
for w 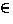 g.adj(v)
g.adj(v) 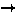 if w
if w  t.nodes and w
t.nodes and w  h
h 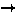 e.old_node := v
e.new_node := w
e.dist := t.dist(v)+ g.cost(v, w)
h.insert(e)
| w
e.old_node := v
e.new_node := w
e.dist := t.dist(v)+ g.cost(v, w)
h.insert(e)
| w 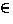 h and g.cost(v,w) + t.dist(v) < h.dist(w)
h and g.cost(v,w) + t.dist(v) < h.dist(w) 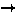 h.changekey(w, (t.dist(v)+g.cost(v,w)), v)
fi
rof
od
end dijkstra
h.changekey(w, (t.dist(v)+g.cost(v,w)), v)
fi
rof
od
end dijkstra