BINARY TREE OPERATIONS
// Precondition Delete must be called with T = root
procedure Delete(Tree T, item x)
if T = NULL 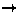 return fi
if x = root->elem
return fi
if x = root->elem 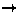 place := root
if place->right = NULL
place := root
if place->right = NULL 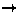 // No right subtree
root := place->left
fi
| x
// No right subtree
root := place->left
fi
| x 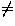 root->elem
(parent, place) := parent_search(T, x)
if parent = NULL
root->elem
(parent, place) := parent_search(T, x)
if parent = NULL 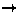 return fi
if place->right = NULL
return fi
if place->right = NULL 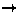 // No right subtree
if x < parent-> elem
// No right subtree
if x < parent-> elem 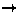 parent-> left := place-> left
| x > parent-> elem
parent-> left := place-> left
| x > parent-> elem 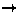 parent-> right := place-> left
fi
fi
fi
next := place->right
if next = NULL
parent-> right := place-> left
fi
fi
fi
next := place->right
if next = NULL 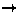 delete place
| next->left = NULL
delete place
| next->left = NULL 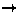 // Right subtree has no left subtree
place->elem := next->elem
place->right := next->right
delete next
| next->left
// Right subtree has no left subtree
place->elem := next->elem
place->right := next->right
delete next
| next->left 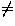 NULL
NULL 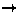 place->elem := del_min(next)
fi
end Delete
place->elem := del_min(next)
fi
end Delete
// Precondition T 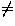 NULL and T->left
NULL and T->left 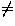 NULL
function del_min(Tree T) returns item
do T->left->left
NULL
function del_min(Tree T) returns item
do T->left->left 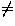 NULL
NULL 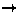 T := T->left
od
val := T->left->elem
ptr := T->left
T->left := T->left->right
delete ptr
return val
end del_min
T := T->left
od
val := T->left->elem
ptr := T->left
T->left := T->left->right
delete ptr
return val
end del_min
// Precondition T 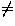 NULL and T->elem
NULL and T->elem 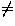 x
function parent_search(Tree T, item x) returns (Tree, Tree)
if x < T->elem and T->left
x
function parent_search(Tree T, item x) returns (Tree, Tree)
if x < T->elem and T->left 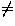 NULL
NULL 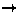 if x = T->left->elem
if x = T->left->elem 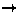 return (T, T->left)
| x
return (T, T->left)
| x 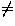 T->left->elem
T->left->elem 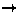 return parent_search(T->left, x)
fi
| x > T->elem and T->right
return parent_search(T->left, x)
fi
| x > T->elem and T->right 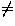 NULL
NULL 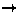 if x = T->right->elem
if x = T->right->elem 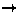 return (T, T->right)
| x
return (T, T->right)
| x 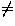 T->right->elem
T->right->elem 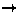 return parent_search(T->right, x)
fi
fi
return (NULL, NULL)
end parent_search
return parent_search(T->right, x)
fi
fi
return (NULL, NULL)
end parent_search
Bernard Waxman
10/7/1997
return fi if x = root->elem
place := root if place->right = NULL
// No right subtree root := place->left fi | x
root->elem (parent, place) := parent_search(T, x) if parent = NULL
return fi if place->right = NULL
// No right subtree if x < parent-> elem
parent-> left := place-> left | x > parent-> elem
parent-> right := place-> left fi fi fi next := place->right if next = NULL
delete place | next->left = NULL
// Right subtree has no left subtree place->elem := next->elem place->right := next->right delete next | next->left
NULL
place->elem := del_min(next) fi end Delete
NULL and T->left
NULL function del_min(Tree T) returns item do T->left->left
NULL
T := T->left od val := T->left->elem ptr := T->left T->left := T->left->right delete ptr return val end del_min
NULL and T->elem
x function parent_search(Tree T, item x) returns (Tree, Tree) if x < T->elem and T->left
NULL
if x = T->left->elem
return (T, T->left) | x
T->left->elem
return parent_search(T->left, x) fi | x > T->elem and T->right
NULL
if x = T->right->elem
return (T, T->right) | x
T->right->elem
return parent_search(T->right, x) fi fi return (NULL, NULL) end parent_search