A very quick survey of population parameters

A statistical population is the collection of all the possible or actual observations of the feature(s) under study. For example, the observable ages of a group of people constitute a statistical population. Suppose that we have 10 people and we collect the following raw data in terms of age: 20, 15, 30, 25, 12, 10, 50, 45, 35, 2. Obviously, in such a raw form, the information is not very useful. Better clarity can be achieved by highlighting the frequency distribution of age. Depending on our interests, we might note that there are 2 people in the age group 0-10; 3 in the group 11-20; 2 in the group 21-30; 1 in the group 31-40; 3 in the group 41-50. We can represent the frequency distribution we have obtained by a histogram:

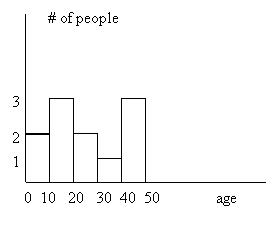
Figure 1

If the population is large (say that 1, 2, and 3 in the frequency coordinate measure thousands) but it has a frequency distribution similar to that of figure 1, it is better to use a frequency curve closely approximating the histogram, as curves can be easily handled once we have their equations (figure 2).

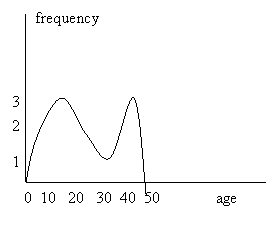
Figure 2

When studying a population, it is often convenient to use population parameters, numbers that provide a summary of the statistical features of the population. There are two major groups of such parameters: central tendency parameters (mean, median, and mode being the most important) and dispersion parameters (range and standard deviation being the most used).

Central tendency parameters

The arithmetic mean is the most common central tendency parameter; it is obtained by summing all the observed values and dividing by the number of observations (the size of the population). For example, if the population is made up of the observations of the ages of 5 people, yielding the values of 20, 35, 15, 5, and 60, the mean age is 125/5 = 25. Sometimes the values of the property under study do not have the same weight. For example, suppose that you want to find your average grade (given in percentage terms) and that you got 80% in a 4-hour course, 90% in a 3 hour course and 100% in a 2 hour course. Obviously, the grade in a 4-hour course has more weight than that in a 2-hour course. Hence, the mean is obtained by summing the weighted grades (each grade times the number of hours) and dividing the total by the number of hours. So, your mean grade (your average) is

(.80 x 4 + .9 x 3 + 1 x 2)/9 = 7.9/9 = .87.

A second commonly used figure is the median, which is the value above and below which lie the same number of observations. For example, in our 5 people group the median is 35 as there are two observed ages (two people) smaller and two larger than 35.

Means are more easily handled than medians. For example, the mean of two combined populations is easily obtained from the means of the component populations by summing the two means and dividing by the number of individuals in the combined population. However, nothing of the sort can be done with medians. Still, medians are much less susceptible to extremes (outlying values) than means. For example, in a group of 5 people a billionaire will dramatically raise the mean income of the group, thus failing to provide a reasonable summary of the average wealth. By contrast, the median will not be unduly influenced by the billionaire’s presence as his wealth will not determine the population center any more than yours.

Finally, the mode is the most frequently occurring observation value. For example, if two people are 30, three 20, one 40 and one 5, the mode is 20, as there are 3 observations of that age value. Typically, when it comes to sizes apparel stores stock items on the basis of the mode, as people with small feet, long legs, and what not, know all too well. Sometimes, a population has more than one mode; when it has two the distribution is bimodal. Populations with more than one mode must be treated carefully as such distributions typically arise when the population is not homogeneous in some significant respect. For example, if we measure height among students, we may find the following distribution (figure 3):

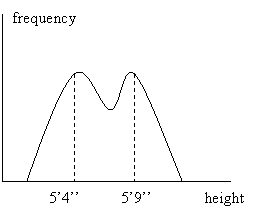
Figure 3

Here the non-homogeneous factor is sex: males are typically taller. The best thing is to break the population into two: measurements of the height of males and measurement of the height of females.

A comparison of mean, median, and mode

Mean, median, and mode do not coincide unless the distribution of the property under study is symmetrical, as in figure 4.

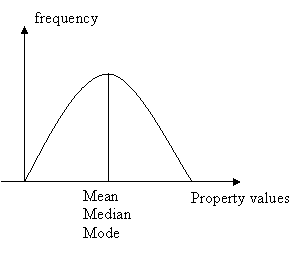
Figure 4

Often, distributions are skewed to the right (figure 5) or skewed to the left (figure 6).

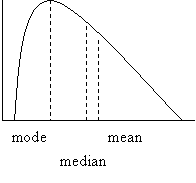
Figure 5

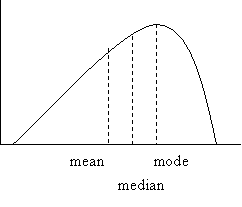
Figure 6

Note that in skewed distributions both median and mean are on the same side of the mode: to its right in right skewed and to its left in left skewed. Note also that the median lies between mode and mean because it is less sensitive to extremes than the mean.

Dispersion parameters

Central value parameters often fail to represent a population properly because do not sufficiently describe the differences among individual observations. For example, if we have 5 people aged 20, 35, 15, 5, and 60, mean age is 125/5 = 25. However, had they been aged 80, 5, 30, 7, and 3, the mean age would still be 25, even if the age distribution would look very different from the previous one. Dispersion parameters remedy this situation by giving us a better idea of the age distribution. The most rudimentary distribution parameter is the range, namely the difference between the highest and the lowest value in the population. For example, the range in the first population is 60-5=55, while that in the second population is 80-3=77.

However, the most important dispersion parameter is the standard deviation. The idea is to measure the difference between each measurement and the mean and then take the population constituted by such differences and calculate the mean. There are various ways of calculating the standard deviation; in practice often one uses the following procedure. First one subtracts the square of the mean from the mean of the squares, thus obtaining the variance. Then one takes the square root of the variation to obtain the standard deviation.

For example, if 5 people are aged 3, 5, 2, 1, 4, first we determine the mean of the squared values:

A= [(1)²+ (2) ² +(3) ² +(4) ² +(5) ²]/5 = 10.8.

Then we determine B, the square of the mean of the values. As the mean is 3

B= 9

Then we calculate the variance V,

V = A – B= 10.8 – 9 = 1.8

Finally, we take the square root of the variance V and obtain the standard deviation:

σ = 1.34.

So, the average difference between an individual age and the mean age is 1.34 years.

Consider now 5 people aged 10, 2, 1, 1, 1; the mean age is, as before 3. Let us calculate the standard deviation:

A= 21.4; B= 9; V= 12.4. Hence,

σ = 3.52.

This tells us that the average difference between an individual age and the mean age is 3.52 years. Hence, the ages in this second group are more spread out than those in the first group. In other words, a small standard deviation indicates that most of the individual ages cluster around the mean; a large standard deviation indicates that most of them are spread out far from the mean.