1. The probability Pr(Q) of a statement (or an event) Q is a real number between 0 and 1.
2. Pr(Tautology) = 1.
ex. Pr[A->(B->A)]=1.
3. Pr(Contradiction) = 0.
ex. Pr(A&-A)=0.
4. If P and Q are logically equivalent (i.e., P<->Q is a tautology),
then Pr(P)=Pr(Q).
ex. Pr(AvB) = Pr[-(-A&-B)].
5. If P is a proposition stating the disjunction of all the possible
outcomes in a certain situation, then Pr(P) = 1.
ex. The probability that a face of the die will come up if the die
is rolled is 1. The probability that heads or tails will come up
if a coin is tossed is1.
6. Pr(-P) = 1-Pr(P).
ex. Suppose we roll a fair die. Then, Pr(2 will come up)=1/6.
Hence, Pr(2 will not come up) = 1-1/6 = 5/6.
7. If P and Q are mutually exclusive (they cannot be true or occur together),
then Pr(PvQ) = Pr(P)+Pr(Q).
ex. Suppose we roll a fair die. Then, Pr(1 comes up or
5 comes up)=Pr(1 comes up)+Pr(5 comes up) = 1/6+1/6 = 2/6 =
1/3.
8. If P and Q are independent, then Pr(P&Q)= Pr(P)xPr(Q)
ex. Suppose we roll a fair die twice. Then Pr(1 comes up on first
roll & 3 comes up on second roll) = Pr(1 comes up on first roll)
x Pr(3 comes up on second roll)=1/6 x 1/6 = 1/36.
An interesting
fact about independence.
9. By Pr(P|Q) we mean the probability of P given that Q. For example,
we indicate with Pr(3|even) the probability that we get 3 given that
we get an even number. Notice that if P and Q are not
independent, Pr(P|Q) is different from Pr(P).
ex. Pr(even) in rolling a fair die is 1/2. But Pr(even|2) is
1. Pr(2)=1/6, but Pr(2|even)=1/3.
ex. Suppose we have an urn with 3 red and 2 black balls and that
we randomly make 2 draws. Then, Pr(B on 2nd draw|R on 1st
draw)=2/4=1/2.
10. Pr(P&Q)=Pr(P)xPr(Q|P).
ex. Suppose we have an urn with 5 black and 5 red balls with
the same probability of being drawn. What's the probability
of drawing 2 red balls? Pr(red on 1st draw & red on 2nd
draw)= Pr(red on 1st draw)xPr(red on 2nd draw|red on 1st draw)= (5/10)x(4/9)=2/9.
Rule 10 can be generalized. Here it's applied to 3 elements:
Pr(P&Q&R)=Pr(P)xPr(Q|P)xPr(R|P&Q).
11. Pr(PvQ) = Pr(P)+Pr(Q)-Pr(P&Q).
ex. Suppose we throw a fair die. What's the probability
of getting an even number or a number less than 3? The
outcomes "even" and "less than 3" are not mutually exclusive (2 is both
even and less than 3!); hence we must apply rule 11. So, Pr(even
or less than 3)= Pr(even)+Pr(less than 3)-Pr(even & less than
3)= (1/2)+(2/6)-(1/6)= 2/3.
Rule 11 can be generalized; here it's applied to 3 elements: Pr(PvQvR)=Pr(P)+Pr(Q)+Pr(R)-Pr(P&Q)-Pr[(PvQ)&R].
12. Pr(P|Q)=Pr(Q|P)x[Pr(P)/Pr(Q)]. This is Bayes' Theorem. For an example, see illustrative exercise 4. Proof of the theorem.
Illustrative exercises.
1.
Find the probability of an event A if the odds it will occur are a)
2 to 1, b) 5 to 11.
a) A occurs 2 times out of 3. Hence, Pr(A)=2/3, and Pr(-A)=1/3.
b) A occurs 5 times out of 16. So, Pr(A)=5/16, and Pr(-A)=11/16.
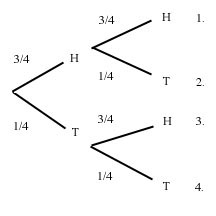
2.
A coin is weighted so that heads (H) is three times more likely to
appear as tails (T). Find Pr(H) and Pr(T). Suppose the
coin is flipped twice. Find: a) Pr(2 heads); b) Pt(2 tails); c) Pr(a
head & a tail).
Solution.

We know that Pr(H)+Pr(T)=1. We are told that Pr(H)=3Pr(T).
Hence, 4Pr(T)=1. So, Pr(T)=1/4 and Pr(H)=3/4.
We can now solve the rest of the problem:
(a)
As the tosses are independent, Pr(H&H)=Pr(H)xPr(H)=(3/4)x(3/4)=9/16.
(branch # 1)
b)
Pr(T&T)=Pr(T)xPr(T)=(1/4)x(1/4)=1/16.
(branch # 4)
c)
There are two ways to get a head and a tail, namely head and tail (branch
# 2) and tail and head (branch # 3). So, Pr(a head and a tail)= Pr[(head
& tails)v(tail & head)]. Since the two alternates are mutually
exclusive, Pr(a head and a tail)=Pr(head &tail)+Pr(tail & head).
Since the two tosses are independent, Pr(head & tail)= Pr(H)xPr(T)
and Pr(tail & head)=Pr(T)xPr(H). So,
Pr(a head and a tail)= (3/4)x(1/4)+(1/4)x(3/4)=3/8.
3.
Of 10 boys in a class, 3 have red hair. If two boys are randomly
selected one after the other, what's the probability that: a) both boys
have red hair; b) neither does; c) at least one does; d) at least one doesn't.
Solution.
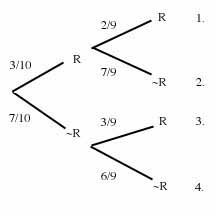
a)
Both boys have red hair just in case we get red hair on the first choice
and red hair on the second (branch # 1). Let's indicate this with
(Ron1 & Ron2). The two choices are not independent. Hence,
Pr(Ron1&Ron2)=Pr(Ron1)xPr(Ron2|Ron1)=(3/10)x(2/9)=1/15.
b)
Neither boy has red hair just in case we get -Ron1&-Ron2 (branch
# 4). (Notice that (-Ron1&-Ron2) is not the same as -(Ron1&Ron2)).
So, Pr(-Ron1&-Ron2)=Pr(-Ron1)xPr(-Ron2|-Ron1)= (7/10)x(6/9)=7/15.
c)
Pr(at least one red)=Pr(-(-Ron1&-Ron2))=1-Pr(-Ron1&-Ron2)=1-7/15=8/15
(branches # 1, 2, or 3).
d)
Pr(at least one not red)= Pr[-(Ron1&Ron2)]=1-Pr(Ron1&Ron2)=1-1/15=14/15
(branches # 2, 3, or 4).
4. We have 3 urns as follows: urn A has 3 red and 5 white marbles; urn
B has 2 red and 1 white marble; urn C has 2 red and 3 white marbles.
An urn is randomly selected, and a marble drawn from the urn. If
the marble is red, what's the probability it came from urn A?
Solution.
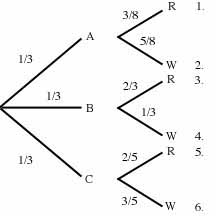
Let's apply Bayes' theorem. Pr(A|R)=Pr(R|A)x[Pr(A)/Pr(R)].
Now,
Pr(R|A)=3/8; Pr(A)=1/3 because the urn is chosen randomly; but what's
Pr(R)? There are 3 mutually exclusive ways of getting a red marble,
namely:
i. choosing A and getting a red marble out
of it.
ii. choosing B and getting a red marble out of it.
iii. choosing C and getting a red marble out of it.
Hence, Pr(R)=Pr(i)+Pr(ii)+Pr(iii)= (1/3)x(3/8)+(1/3)x(2/3)+(1/3)x(2/5)=173/360.
So, Pr(A|R)=45/173.
Some extra facts about probability (1, 2, and 3 are important)
1. Pr(A&B) is less then or at most equal to Pr(A)
2. Pr(AvB) is greater than or at least equal to Pr(A)
3. If B follows from A (i.e. “B; Hence A’ is valid), then Pr(B) is greater than or at least equal to Pr(A)
4. Pr[(AvB)|H]=Pr(A|H)+Pr(B|H)-Pr((A&B)|H)
There's no nice rule for Pr[H|(AvB)]
5. Pr(A&B|H)=Pr(A|H)xPr(B|(A&H))
6. Pr(-A|H)=1-Pr(A|H)
There's no nice rule for Pr(H|-A)
7. If A is a tautology, Pr(A|B)=1 if Pr(B) is different from 0; Pr(B|A)=Pr(B)
8. If A is a contradiction, Pr(A|B)=0 if Pr(B) is different from 0; Pr(B|A) is undefined.
9. Pr(P&-Q)=Pr(P)-Pr(P&Q)
10. Pr(-P&-Q)=1+Pr(P&Q)-Pr(P)-Pr(Q)