Probability Density

The mass density d of a body is mass per unit length.  Consequently, if a wire’s density is constant at d=1kg/m and its length is 3 meters, the wire’s total mass will be 3kg, namely, the area of the figure between d‘s plot and the x-axis from 0 to 3 (Fig. 1). 

Text Box: d
 

 

 

 


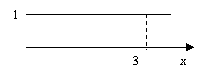
Figure 1

 

Even if the plot of the density of more complex than the one we just considered, the point remains the same: to determine the mass of the wire between 0 and 3, we reckon the area under d between 0 and 3. 

Consider now a particle M moving to the right along the x-axis from  to l.  At time t=0, M is at position 1; let us suppose that its speed is given as a function of position:

v=1/x.                                                                                                  (4.1.1)

In other words, the farther ahead M moves, the slower its velocity is, according to (4.1.1).   For example, at point 1, M’s velocity is 1 meter per second; at point 2, it is 1/2 meter per second, and so on. Imagine taking snapshots at random times while M goes from 1 to l.  Where will the bulk of the snapshots depict M to be?  Close to 1, to l, or to the middle?  Upon reflection the answer is easy.  M starts with velocity vo=1 and then it slows down as it progresses to higher values of x until it gets to l with velocity is.  Hence, if we divide the interval  into equal intervals dx, M will spend less time in the early intervals (those closer to 1) and more in the later ones (those close to l).  Consequently, the snapshots will mostly depict M being closer to l than to 1. 

Let us make the previous considerations more precise.  The probability that M will be observed in an interval dx is directly proportional to the amount of time M takes in traversing it.  In other words, the probability that M will be observed in an interval dx is inversely proportional to the speed v with which M traverses it, and is therefore equal to C/v, where C is a constant of proportionality.  Using (4.1.1), we express this by

,                                                                                                           (4.1.2)

where Pd is the position probability density.  As mass density measures mass per unit of length, so position probability density measures probability per unit of length.  The former is proportional to the amount of matter per unit of length, the latter to the amount of time the particle spends in traversing a unit of length.

 

 

 

 

 


                                                                       

 

 


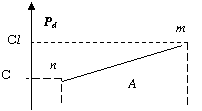
Figure 2

The probability that M is between 1 and l is given by the area A of the figure under nm, namely, the trapeze 1lmn in figure 2.  From classical geometry, we obtain

.                                                                                       (4.1.3)

However, the particle must be somewhere between 1 and l, and therefore.  Hence, a bit of algebra gives us

 .                                                                                                      (4.1.4)

Consequently,

.                                                                                                  (4.1.5)

The process whereby one determines the constant C is called “normalization”.  It is demanded by the principle that the sum of all the mutually exclusive possibilities of a situation must be equal to one. 

Now let us plug in some figures.  Suppose that .  Then, from (4.1.5) we obtain

.                                                                                                        (4.1.6) 

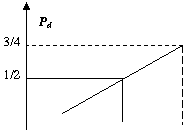
Hence, the probability that M is between 1 and 2 is given by the area under  between 1 and 2 (Fig. 3).

 

 

 

 

 

 


Text Box: 1/4                                                                       

 


Figure 3

Consequently,

,                                                                                                     (4.1.7)

while the probability that M is between 2 and 3 is

.                                                                                                     (4.1.8)

As we expected, since M slows down, it is more likely to be observed after the midpoint than before.  Notice that , as it should be.

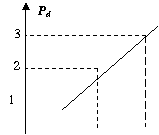
It is instructive to see what happens if we do not normalize.  Then we would have

;                                                                                                           (4.1.9)

its graph would be (Fig. 4)

 

 

 

 

 


                                                                       

 


Text Box: 2 Text Box: 3Text Box: x 

Figure 4

Then, Pr(1,2) = 3/2 and Pr(2,3) = 5/2, both of which is impossible, as no probability can be greater than 1.  In sum, the price of not normalizing is abandoning probability.  Note, however, that the ratio between the two “probabilities” obtained without normalization, namely, 3/5, is the same as that among the true probabilities obtained after normalizing: relative ratios can be obtained without normalizing.