Phil 207 (Dr. Vailati) Probability calculus rules.

1. The probability Pr(Q) of a statement (or an event) Q is a real number between 0 and 1.

2. the probability of a tautology (a statement that has to be true no matter what, such as "it rains or it does not rain") is 1.

3. The probability of a contradiction ( a statement that has to be false no matter what, such as "it rains and it does not rain") is 0.

NOTE: the negation (direct denial) of a contradiction is a tautology and vice versa. The safest way to deny a statement is to prefix it with "it is not that case that". For example, the negation of "it rains" is "it is not the case that it rains" or, more simply "it does not rain". Note that the negation of "all that shines is gold" is not "all that shines is not gold", since some gold shines, but "not all that shines is gold", since some shining things are not gold. To play it safe, it's better to say "It is not the case that all that shines is gold". Given a statement A, we represent its negation by "-A".

4. If P and Q are logically equivalent (thay amount to the very same thing, such as "John is a bachelor" and "John is an unmarried male", or "it rains" and "John is short and it rains, or John is not short and it rains"), then Pr(P)=Pr(Q).

5. If P is a proposition stating all the possible outcomes in a certain situation ("Either A, or B, or C, etc"), then Pr(P) = 1.
ex. The probability that a face of the die will come up if the die is rolled is 1. The probability that heads or tails will come up if a coin is tossed is1.

6. Pr(-P) = 1-Pr(P).
ex. Suppose we roll a fair die. Then, Pr(2 will come up)=1/6. Hence, Pr(2 will not come up) = 1-1/6 = 5/6.

7. If P and Q are mutually exclusive (they cannot be true or occur together), then Pr(P or Q) = Pr(P)+Pr(Q).
ex. Suppose we roll a fair die. Then, Pr(1 comes up or 5 comes up)=Pr(1 comes up)+Pr(5 comes up) = 1/6+1/6 = 2/6 = 1/3.

NOTE: From now on, we may express "or" with "v", so that "P or Q" becomes "PvQ".

8. If P and Q are independent, then Pr(P and Q)= Pr(P)xPr(Q)

NOTE: From now on, instead of using "and", we may use "&", so that "P and Q" may become "P&Q".
ex. Suppose we roll a fair die twice. Then Pr(1 comes up on first roll & 3 comes up on second roll) = Pr(1 comes up on first roll) x Pr(3 comes up on second roll)=1/6 x 1/6 = 1/36.
Some interesting facts.

9. By Pr(P|Q) we mean the probability of P given that Q. For example, we indicate with Pr(3|even) the probability that we get 3 given that we get an even number.   Notice that if P and Q are not independent, Pr(P|Q) is different from Pr(P).
ex. Pr(even) in rolling a fair die is 1/2. But Pr(even|2) is 1.   Pr(2)=1/6, but Pr(2|even)=1/3.
ex. Suppose we have an urn with 3 red and 2 black balls and that we randomly make 2 draws. Then, Pr(B on 2nd draw|R on 1st   draw)=2/4=1/2.

10. Pr(P&Q)=Pr(P)xPr(Q|P).
ex. Suppose we have an urn with 5 black and 5 red balls with the same probability of being drawn. What's the probability of drawing 2 red balls? Pr(red on 1st draw & red on 2nd draw)= Pr(red on 1st draw)xPr(red on 2nd draw|red on 1st draw)= (5/10)x(4/9)=2/9.
Rule 10 can be generalized. Here it's applied to 3 elements: Pr(P&Q&R)=Pr(P)xPr(Q|P)xPr(R|P&Q).

11. Pr(PvQ) = Pr(P)+Pr(Q)-Pr(P and Q).
ex. Suppose we throw a fair die. What's the probability of getting an even number or a number less than 3? The outcomes "even" and "less than 3" are not mutually exclusive (2 is both even and less than 3!); hence we must apply rule 11. So, Pr(even or less than 3)= Pr(even)+Pr(less than 3)-Pr(even & less than 3)= (1/2)+(2/6)-(1/6)= 2/3.
Rule 11 can be generalized; here it's applied to 3 elements: Pr(PvQvR)=Pr(P)+Pr(Q)+Pr(R)-Pr(P&Q)-Pr[(PvQ)&R].

12. Pr(P|Q)=Pr(Q|P)x[Pr(P)/Pr(Q)]. This is Bayes' Theorem. For an example, see illustrative exercise 4. Proof of the theorem.

Illustrative exercises.
1.
Find the probability of an event A if the odds it will occur are a) 2 to 1, b) 5 to 11.
a) A occurs 2 times out of 3. Hence, Pr(A)=2/3, and Pr(-A)=1/3.
b) A occurs 5 times out of 16. So, Pr(A)=5/16, and Pr(-A)=11/16.

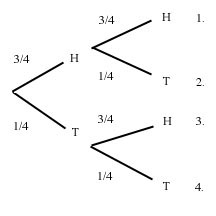
2.
A coin is weighted so that heads (H) is three times more likely to appear as tails (T). Find Pr(H) and Pr(T). Suppose the coin is flipped twice. Find: a) Pr(2 heads); b) Pt(2 tails); c) Pr(a head & a tail).
Solution.

We know that Pr(H)+Pr(T)=1. We are told that Pr(H)=3Pr(T). Hence, 4Pr(T)=1. So, Pr(T)=1/4 and Pr(H)=3/4.
We can now solve the rest of the problem:
(a)
As the tosses are independent, Pr(H&H)=Pr(H)xPr(H)=(3/4)x(3/4)=9/16.
(branch # 1)
b)
Pr(T&T)=Pr(T)xPr(T)=(1/4)x(1/4)=1/16.
(branch # 4)
c)
There are two ways to get a head and a tail, namely head and tail (branch # 2) and tail and head (branch # 3). So, Pr(a head and a tail)= Pr[(head & tails)v(tail & head)]. Since the two alternates are mutually exclusive, Pr(a head and a tail)=Pr(head &tail)+Pr(tail & head). Since the two tosses are independent, Pr(head & tail)= Pr(H)xPr(T) and Pr(tail & head)=Pr(T)xPr(H). So,
Pr(a head and a tail)= (3/4)x(1/4)+(1/4)x(3/4)=3/8.

3.
Of 10 boys in a class, 3 have red hair. If two boys are randomly selected one after the other, what's the probability that: a) both boys have red hair; b) neither does; c) at least one does; d) at least one doesn't.
Solution.

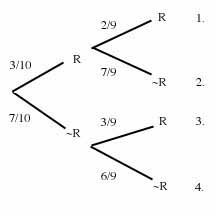
a)
Both boys have red hair just in case we get red hair on the first choice and red hair on the second (branch # 1). Let's indicate this with (Ron1 & Ron2). The two choices are not independent. Hence,
Pr(Ron1&Ron2)=Pr(Ron1)xPr(Ron2|Ron1)=(3/10)x(2/9)=1/15.
b)
Neither boy has red hair just in case we get -Ron1&-Ron2 (branch # 4). (Notice that (-Ron1&-Ron2) is not the same as -(Ron1&Ron2)). So, Pr(-Ron1&-Ron2)=Pr(-Ron1)xPr(-Ron2|-Ron1)= (7/10)x(6/9)=7/15.
c)
Pr(at least one red)=Pr(-(-Ron1&-Ron2))=1-Pr(-Ron1&-Ron2)=1-7/15=8/15 (branches # 1, 2, or 3).
d)
Pr(at least one not red)= Pr[-(Ron1&Ron2)]=1-Pr(Ron1&Ron2)=1-1/15=14/15 (branches # 2, 3, or 4).

4. We have 3 urns as follows: urn A has 3 red and 5 white marbles; urn B has 2 red and 1 white marble; urn C has 2 red and 3 white marbles. An urn is randomly selected, and a marble drawn from the urn. If the marble is red, what's the probability it came from urn A?
Solution.

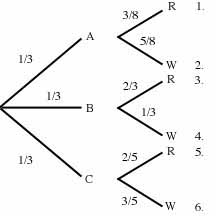
Let's apply Bayes' theorem. Pr(A|R)=Pr(R|A)x[Pr(A)/Pr(R)]. Now,
Pr(R|A)=3/8; Pr(A)=1/3 because the urn is chosen randomly; but what's Pr(R)? There are 3 mutually exclusive ways of getting a red marble, namely:
i.     choosing A and getting a red marble out of it.
ii.    choosing B and getting a red marble out of it.
iii.   choosing C and getting a red marble out of it.

Hence, Pr(R)=Pr(i)+Pr(ii)+Pr(iii)= (1/3)x(3/8)+(1/3)x(2/3)+(1/3)x(2/5)=173/360.
So, Pr(A|R)=45/173.

Some extra facts about probability (1, 2, and 3 are important)

1. Pr(A&B) is less then or at most equal to Pr(A)

2. Pr(AvB) is greater than or at least equal to Pr(A)

3. If B follows from A (i.e. “B; Hence A’ is valid), then Pr(B) is greater than or at least equal to Pr(A)

5. Pr(A&B|H)=Pr(A|H)xPr(B|(A&H))

6. Pr(-A|H)=1-Pr(A|H)
There's no nice rule for Pr(H|-A)

7. If A is a tautology, Pr(A|B)=1 if Pr(B) is different from 0; Pr(B|A)=Pr(B)

8. If A is a contradiction, Pr(A|B)=0 if Pr(B) is different from 0; Pr(B|A) is undefined.

9. Pr(P&-Q)=Pr(P)-Pr(P&Q)

10. Pr(-P&-Q)=1+Pr(P&Q)-Pr(P)-Pr(Q)

Proofs of (1)-(3).