A very short intro to
evolutionary game theory
Game theory developed to study the strategic interaction among rational self regarding players (players seeking to maximize their own payoffs). However, by the early 1970’s the theory underwent a transformation and part of it morphed into evolutionary game theory, which allows to increase our understanding of dynamical systems, especially in biology and, more recently, in psychology and the social sciences, with significant ramifications for philosophy. The players are not required to be rational at all, but only to have (perhaps hardwired) strategies that are passed on to their progeny. In short, the notion of player is displaced by that of strategy, and consequently the notion of a player’s knowledge, complete or incomplete, is dispensed with. What drives systems is not the rationality of the players but the differential success of the strategies.
As before, we consider only two-player games. A game with strategies s1,…..sn for both players is strategy symmetric (symmetric, in brief) if:
- when i=j the payoffs for the two identical strategies are the same, which means that along the main diagonal (top left to bottom right) the payoffs in each box are the same
- the payoffs in the remaining boxes on one side of the main diagonal are mirror images of their counterparts on the other side.
For example, The Prisoners’ Dilemma is a symmetric game. Along the main diagonal (top left to bottom right), the payoffs are the same in each box that is, (1,1) and (6,-6); moreover, we have (-10, 10) in the top right box and (10, -10) in the bottom left, which are mirror images of each other.
|
|
S |
C |
|
S |
1;1 |
10;-10 |
|
C |
-10;10 |
-6;-6 |
A symmetric matrix can be simplified by writing only the payoffs of the row strategies, as those of the column strategies can be easily obtained by exploiting the symmetry of the game. So, the previous matrix can be simplified as
|
|
S |
C |
|
S |
1 |
10 |
|
C |
-10 |
-6 |
For simplicity, from now on we only deal with symmetric games.
Evolutionary Stable
Strategies (ESS)
An important concept of evolutionary game theory is that of evolutionarily stable strategy (ESS). To understand it, we need some new notions.
Imagine now that we keep repeating a symmetric game (each round is called a ‘stage game’) with random pairing in an infinite population in which the only relevant consideration is that successful players get to multiply more rapidly than unsuccessful ones. (The demand that the population is theoretically infinite excludes random drift). Suppose that all the players (the incumbents) play strategy X, which can be a pure or a mixed strategy. If X is stable in the sense that a mutant playing a different strategy Y (pure or mixed) cannot successfully invade, then X is an ESS. More precisely, if by EP(A,B) we understand the payoff resulting from playing strategy A against strategy B, X is an ESS if either
- E(X,X)>E(Y,X),
that is, the payoff for playing X against X is greater than that for playing any other strategy Y against X
or
- E(X,X)=E(Y,X) and E(X,Y)>E(Y,Y)
that is, the payoff of playing X against itself is equal to that of playing Y against X but the payoff of playing Y against Y is less than that of playing X against Y.
Note that either (1) or (2) will do.
Obviously, if (1) obtains, the Y invader typically loses against X, and therefore it cannot persist. If (2) obtains, the Y invader does as well against X as X itself, but it loses to X against other Y invaders, and therefore it cannot multiply. In short, Y cannot successfully invade a population of X’s.
For example, consider Stag Hunt and a population of Stags. Then Hare cannot invade because EP(S,S) > EP(H,S), which is condition (1) above.
(Question: Is Hare an ESS?)
It is possible to introduce a strategy that is stronger than an ESS, namely, an unbeatable strategy. Strategy X is unbeatable if, given any other strategy Y
E(X,X)>E(Y,X) and E(X,Y)>E(Y,Y).
An unbeatable strategy is the most powerful strategy there is because it strictly dominates any other strategy; however, it is also rare, and therefore of very limited use. For example, in Stag Hunt S, although an ESS, is not unbeatable because EP(S,H) < EP(H,H).
Two final points about ESS should be noted:
- Every ESS is a strategy in a Nash equilibrium in the stage game, although the reverse is not true (not all Nash equilibriums are made up of ESS).
- An ESS can be displaced since it can have a lower payoff than one of two or more simultaneously invading strategies. However, an ESS cannot be displaced by one invading strategy
Evolutionary Dynamics
We just saw that in a population in which an ESS has already taken over, invasion does not occur successfully. However, under which conditions does a strategy take over in a population? What happens if a game in an infinite population is repeated indefinitely? The answer comes from evolutionary dynamics, which studies the behavior of systems evolving under some specific evolutionary rule. The basic idea here is that of the replicator, an entity capable of reproducing, that is, of making (relevantly) accurate copies of itself. Examples of replicators are living organisms, genes, strategies in a game, ideas (silly or not), as well as political, moral, religious, or economic customs (silly or not). A replicator system is a set of replicators in a given environment together with a given pattern of interactions among them. An evolutionary dynamics of a replicator system is the process of change of the frequency of the replicators brought about by the fact that replicators which are more successful reproduce more quickly than those which are less successful. Crucially, this process must take into account the fact that the success, and therefore the reproduction rate, of a replicator is due in part to its distribution (proportion) in the population. For example, when playing Chicken, although drivers do well against swervers, in a population of drivers a single swerver does better than anybody else. So, it will reproduce more quickly the others. However, at some point or other, there will be enough swervers that the drivers will start to do better again. It would be nice to know whether there is some equilibrium point, and if so what it is.
Since the differential rate of reproduction determines the dynamics of the system, we need to be more precise and specify what we mean by ‘more quickly’. This is determined by the dynamics of the system; the one we are going to study is replicator dynamics. There are other models that plausibly apply to evolution, but replicator dynamics is the easiest and the most often used, at least at a first approach. Replicator dynamics makes two crucial assumptions:
- There is no random drift; in other words, there are no random events interfering with the results of differential fitness, the fact that some individuals are favored in relation to others. In small populations, random drift is a significant dynamical force, an issue we shall have to deal with later.
- The interactions among players (strategies) are random; that is, the probability of strategy S meeting strategy H is the frequency of H. For example, if 1/3 of the population is H, the probability of an individual playing an H is 1/3 and that of playing an S is 2/3.
In addition, we shall restrict ourselves to studying repeated games whose stage games are symmetric and have only two players, so that the math remains easy.
To understand replicator dynamics, we need to introduce a few notions.
The first is that of rate of change. Experience teaches that things often change at different rates. For example, sometimes accidentally introduced species multiply more quickly than native species: in other words, their rate of growth is greater than that of native species, and this typically results in a decline of the natives. So, if at the moment of introduction the frequency of the non-native species was p and that of the native species was q= 1-p, with q >> p, after some time the situation may change and become p>q. This means that p has a positive rate of change (it increases) while q has a negative rate of change (it decreases). Mathematically, we express this by writing
D(p) > 0 and D(q) <0,
where D(p) (the derivative of p with respect to time) means ‘the rate of change of p’, and similarly for q.
So, suppose a population P increases by 1/3 every second; then if in the beginning p=100, then after one second, p1=100 + 1/3(100)= 130, after 2 seconds, p2= p1 +1/3(p1) = 130 +1/3(130), and so on.
The second notion is that of expected payoff of a pure strategy. Suppose a pure strategy s is played against strategies S1, …,Sn, and that Pr(Si) is the probability that Si is played. If by EP(s) we understand the expected payoff of strategy s, then,
EP(s)=E(s,S1) Pr(S1) + …..+ E(s,Sn) Pr(Sn).
That is, if by Si we denote a generic S, the expected payoff of s is the sum of the payoffs of s against each of the Si times the probability that Si is played. For example, consider the matrix below,
|
|
S |
H |
|
s |
4 |
1 |
|
h |
2 |
3 |
and suppose that in the columns S is played 1/3 of the times and H 2/3 of the times. Then EP(s) is
4(1/3) + 1(2/3) = ½.
EP(h) is
2(1/3) + 3(2/3) = 8/3.
The third notion is that of average payoff of a set of strategies, and to understand this, we need to consider the notion of the mean. Suppose that in a group of boxes, 1/3 weigh 30 kilos, ½ weigh 20 and 1/6 weigh 60. Then the average weight ĀW (notice the bar above ‘A’) is:
ĀW =30x1/3 + 40x1/2 + 30x1/6 = 10+20+5=35.
In words, the average weight is the sum of all the weights, each multiplied by its frequency. (Since 1/3 of the boxes weigh 30 kilos, we multiply 30 by 1/3, and so on).
Similarly, if S(tag) and H(are) are the two available strategies, the average payoff is
ĀEP= EP(S)Pr(S) + EP(H) Pr(H).
For example, consider the following Stag Hunt matrix, and suppose that Pr(S)=p, so that Pr(H)=1-p.
|
|
S |
H |
|
S |
3 |
0 |
|
H |
2 |
1 |
Then, the EP of S, when played with frequency p against another S and with frequency 1-p against an H is:
EP(S)=3p+0(1-p)=3p.
Analogously, the EP of H, when played with frequency p against another S and with frequency 1-p against another H is
EP(H)=2p+1(1-p)=p+1.
So, the average expected payoff is EP(S) times the probability that S is played plus EP(H) times the probability that H is played:
ĀEP=EP(S) x Pr(S) + EP(H) x Pr(H)= 3p2 + (p+1)(1-p)= 2p2 +1.
In replicator dynamics, if Pr(S)=p, the dynamical equation (the equation ruling the behavior of the system through time) is:
D(p) = [EP(S) – ĀEP)p
In other words,
the rate of change of the frequency of a strategy (in this case S), is determined by the difference between the expected payoff of S and the average payoff.
Consequently, when S’s expected payoff is greater than the average payoff, the frequency of S increases, and when it’s smaller then the frequency of S decreases. Hence, in our example we have:
D(p) = [EP(S) – ĀEP)p = [-2p2 +3p-1]p.
Obviously, when D(p)=0 the frequency of S (that is, p) does not change. The values of p for which the frequency of S does not change are called “fixed points”. So, let us find the fixed points in our example, that is, let us find when
[-2p2 +3p-1]p=0.
Obviously, one fixed point is p=0. For the other two, we need to solve
-2p2 +3p-1=0,
which gives p=1 and p=1/2. So, when p=0, or p=1, or p=1/2, the frequency of S does not change. But what happens when p is not equal to any of the three fixed points? Let us study the plot of
D(p)=[-2p2 +3p-1]p.
As we can verify by substituting 1/3 for p, when 0<p<1/2 the rate of growth of p is negative, and when 1/2<p<1 the rate of growth of p is positive (just substitute 2/3 for p, for example). Since for p=1/2 the growth rate of p is zero, the plot looks (more or less) like this:
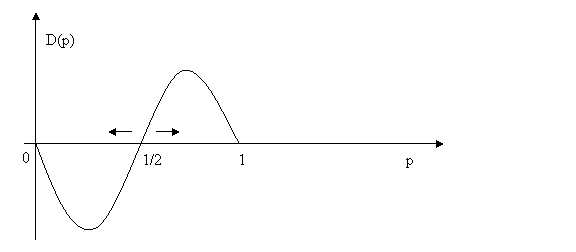
If at some time p<1/2, as the growth rate is negative p will eventually become zero, that is, the strategy S will disappear; by contrast, if at some time p>1/2, then S will become fixated, that is it will remain the only strategy (H will disappear). If p=1/2, then exactly half of the population will play S and half H. However, this equilibrium is not stable in the sense that even a minor deviation from it will push one of H or S to extinction and the other to fixation, both of which are stable.
The interval (0,1/2) is the basin of attraction of which H is the attractor, and the interval (1/2,1) that of S. The fixed points p=0 and p=1 are asymptotically stable because each is an attractor of a basin of attraction. If the basin of attraction of an attractor contains the whole interval in which p is defined, or at least all the interior points, then the attractor is globally stable. In our example, no fixed point is globally stable. 1/2 is the interior fixed point and, as we saw, it is unstable.
Replicator dynamics of
a generalized 2 by 2 symmetric game
A symmetric game with 2 strategies, A and B, can be represented by the following payoff matrix, where the payoff are those of the row strategies:
|
|
A |
B |
|
A |
a |
b |
|
B |
c |
d |
It turns out that the replicator dynamics does not change if in any column we add or subtract the same quantity from all the boxes. Hence, we can reduce the matrix by subtracting c from the first column and d from the second, obtaining
|
|
A |
B |
|
A |
a-c |
b-d |
|
B |
0 |
0 |
To find the interior point:
· Reduce the matrix by setting strategy B’s payoffs equal to zero and modifying the other payoffs accordingly
· Solve EP(A) = 0.
There are five possible cases in a game:
- A dominates B: a≥c and b≥d, where at least one of the inequalities is strict. It turns out that replicator dynamics wipes out dominated strategies; hence, A will reach fixation.
- B dominates A: c≥a and d≥b, where at least one of the inequalities is strict. Since A is dominated, B reaches fixation.
- A is the best response to A and B to B. (In other words, your best bet is to mimic the moves of your opponent). Then, a>c and d>b, so that in the reduced matrix a-c > 0 and b-d < 0. The interior point determines an unstable equilibrium. The system is bistable, meaning that one of the two strategies will reach fixation, but which does depends on the initial strategy distribution, that is, the initial value of p. The strategy that has the larger basin of attraction is risk dominant: if the initial distribution is random, on average the risk dominant strategy will reach fixation more often.
- A is the best response to B and B the best response to A, that is, b>d and c>a, so that in the reduced matrix a-c < 0 and b-d > 0. In other words, you best bet is to do the opposite of what your opponent does. Then the interior fixed point determines a globally stable equilibrium: the system will converge to it independently of the original distribution. A and B will coexist in a predetermined fixed ratio. The system is ergodic, meaning that the final state is independent of the initial conditions.
- A and B are neutral: a=c and b=d. Then selection is neutral, D(p)=0 at all times, and the original strategy distribution p will be preserved.
There are some interesting connections between dominance, Nash equilibriums, ESS, and replicator dynamics.
- Nash equilibriums determine fixed points. However, fixed points such as p = 1 are not associated with a Nash equilibrium.
- If the fixed point p is associated with an ESS, then p is asymptotically stable. The converse need not be true.
- The fixed point p is associated with an ESS which uses every strategy with positive probability (that is, greater than zero) if and only if p is globally stable.
- No strongly dominated strategy survives replicator dynamics.
Exercises
1. Determine the evolution of the following game under replicator dynamics.
|
S |
H |
|
|
S |
5 |
0 |
|
H |
2 |
2 |
2. Determine the evolution of the following game under replicator dynamics.
|
A |
B |
|
|
A |
3 |
1 |
|
B |
4 |
0 |
Determine the evolution of the following version of Chicken under replicator dynamics (D= drive straight; S= swerve).
|
D |
S |
|
|
D |
-5 |
3 |
|
S |
-2 |
0 |
4.
Determine the evolution of the following game under replicator dynamics. Does the game look familiar?
|
S |
C |
|
|
S |
1 |
-5 |
|
C |
4 |
0 |
Hint. Before you launch into calculations, ask yourself whether the one-shot game above is strong dominance solvable. Would you think that strongly dominated strategies survive replicator dynamics?
5.
Determine the evolution of the following game under replicator dynamics.
|
A |
B |
|
|
A |
3 |
1 |
|
B |
3 |
1 |
Rock, Paper, Scissors
Uta Stansburiana is a lizard whose morph distribution can be understood by considering the game of Rock-Paper-Scissors, a particularly interesting case of a game with three strategies. However, before we do that we need to look at ternary plots, a common way to represent the phase space of such games.
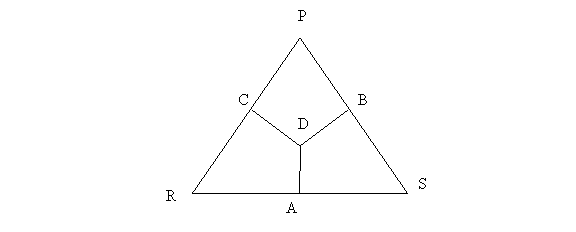
Consider the equilateral triangle RSP and the segments DA, DB, and DC, which are the distances of D from side RS, SP, and PR, respectively. Vertex R represents the strategy Rock, vertex S Scissors and vertex P Paper. Any point D in the triangle, including the interior area, sides, and vertices, represents a probability distribution of the strategies, with distance DA representing the frequency of Paper, DB that of Rock, and DC that of Scissors. Note that any two of such distances fully determines the strategy distribution. The distance between a vertex and the opposite side is normalized, which means that when point D coincides with a vertex, that vertex’s strategy is the only left. For example, when D coincides with P the frequency of P is 1. By the same token, if D is located on a side, then the frequency of the strategy of the opposing vertex is zero. For example, if D is located on RS, then the frequency of P is zero.
Rock-Paper-Scissors is a game in which Rock (R) beats Scissors (S), Scissors beats Paper (P) and Paper beats Rock, so that the relation ‘X beats Y’ is intransitive.
Assuming that winning and losing represent invasion rates of one species or one morph against another, the generalized matrix for the game can always be reduced to
|
|
R |
S |
P |
|
R |
0 |
a |
-b |
|
S |
-c |
0 |
d |
|
P |
e |
-f |
0 |
Table 1
where the invasion rate is between and including 0 and 1, with 1 representing the case in which the winning strategy completely replaces the defeated one. For example, if a=.6, then R wins (invades) against S 60% of the times. Note that when a=c, b=e, and d=f the game is zero sum; moreover, when a=b=c=d=e=f=1 the classic RPS game obtains.
In the replicator dynamics of Rock, Scissors, Paper the following is true:
- There is only one internal fixed point (an equilibrium point)
- If p is the frequency of P, r that of R and s that of S at the internal fixed point, then the following holds:
I. p=αa, r=αd, s=αe,
II. with α = (a+d+e)-1, which is the inverse of the sum of the invasion rates.
(I)-(II) entail that the frequency of a strategy at the interior equilibrium is not determined by its own invasion rate but by that of the strategy it invades. For example, the frequency of P is proportional to a, the invasion rate of R. Consequently, if a strategy has the highest invasion rate, then its invader has the highest frequency at equilibrium, and if it has the lowest invasion rate, then its invader has the lowest frequency.
- There are three cases based on the value of the matrix determinant Δ:
- If Δ < 0, then the interior fixed point is an unstable center, with trajectories spiraling out asymptotically to the sides.

- If Δ = 0, then the interior fixed point is a center of stable orbits circling around it.

- If Δ > 0, then the interior fixed point is globally stable, with the orbits exhibiting damped oscillations convergint to it.
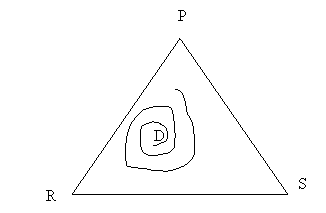
In computer simulations, when Δ < 0:
- The orbits spiral out towards the sides eventually touching one of the sides. (This is due to computer rounding)
- The species with the lowest frequency at the interior equilibrium has the lowest frequency along every orbit, and consequently the greatest probability of extinction.
Hence, strategy X with the lowest invasion rate is the one most likely to survive, as its invader will vanish, with the result that X will displace that remaining strategy. In short, the game results in the survival of the weakest, if by that we understand that which is least successful at invading. In practice, if strategies are replaced by species or morphs, and a disease, or human intervention, weakens one of them by diminishing its invasion rate, then that species or morph is the most likely to survive.
As an example of RPS, consider the following matrix, where payoffs are invasion rates:
|
|
R |
S |
P |
|
R |
0 |
.2 |
-.4 |
|
S |
-.5 |
0 |
.8 |
|
P |
.3 |
-.6 |
0 |
Then, α = 10/13, so that r = 8/13, s = 3/13, and p = 2/13. As the determinant Δ = (.4x.5x.6 –.2x.8x.3) > 0, it follows that under replicator dynamics the interior equilibrium is globally stable.
Many species or morphs from unicellular organisms to vertebrates, can be studied using RPS, including E. Coli (a microbe in our guts), Uta Stansburiana (a California lizard and the first species to which RPS was successfully applied), Ischnura Elegans (a damselfly), and Paracercis Sculpta (a marine isopod). More generally, RPS can be used to investigate any system in which ‘power’ relations are intransitive.
For an interesting and entertaining lecture on evolutionary game theory, watch this public lecture by Prof. Nowak at Harvard.